目的
今回は、reluの正答率が高いのは、0以下の時値が0で傾きも0であることに起因していると仮説を立てその検証を行う。
条件
なお検証用のプログラムこれまでと同じ
import tensorflow as tf
from tensorflow.keras.datasets import cifar10
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout
from tensorflow.keras.utils import to_categorical
import time
# CIFAR-10 データの読み込み
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
# 正規化
x_train = x_train.astype('float32') / 255
x_test = x_test.astype('float32') / 255
# ラベルを one-hot エンコーディング
y_train = to_categorical(y_train, 10)
y_test = to_categorical(y_test, 10)
# モデルの構築
model = Sequential([
Conv2D(32, (3, 3), activation='relu', padding='same', input_shape=(32, 32, 3)),
Conv2D(32, (3, 3), activation='relu'),
MaxPooling2D(2, 2),
Dropout(0.25),
Conv2D(64, (3, 3), activation='relu', padding='same'),
Conv2D(64, (3, 3), activation='relu'),
MaxPooling2D(2, 2),
Dropout(0.25),
Flatten(),
Dense(512, activation='relu'),
Dropout(0.5),
Dense(10, activation='softmax')
])
# モデルのコンパイル
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
# モデルの訓練
history = model.fit(x_train, y_train, batch_size=64, epochs=50, validation_data=(x_test, y_test), verbose=2)
# モデルの評価
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
print("time", time.time() - start_t)
loss = history.history['loss']
accuracy = history.history['accuracy']
val_loss = history.history['val_loss']
val_accuracy = history.history['val_accuracy']
import pandas as pd
df = pd.DataFrame({'loss': loss, 'accuracy': accuracy, 'val_loss': val_loss, 'val_accuracy': val_accuracy})
df.to_csv('fime_name.csv', index=False)を使用する。
今回は、以前使用した平方根を180対称にした関数とtanhで0以下は0にするという関数を作成し、元の関数と比較する。それぞれ、rectified_sqrt, rectified_tanhとする。それぞれの関数は、以下のようになる。
tanh
def rectified_tanh(x):
return tf.where(x <= 0,
tf.cast(0, x.dtype),
tf.nn.tanh(x))平方根
def rectified_sqrt(x):
return tf.where(x <= 0,
tf.cast(0, x.dtype),
tf.sqrt(x + g_aa) - tf.sign(x)*g_a)結果
reluとも比較するため3つの関数の結果を並べて示す。
accuracy, lossは学習用データの結果、val_accuracy, lossはテストデータの結果
| relu | tanh | rectified_tanh | |
| function | 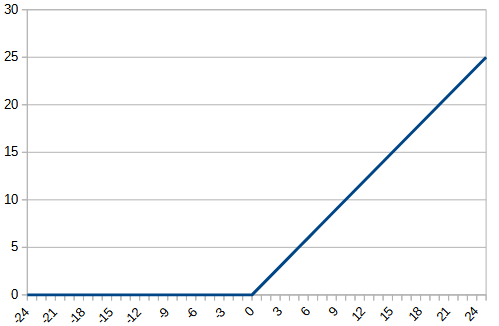 | 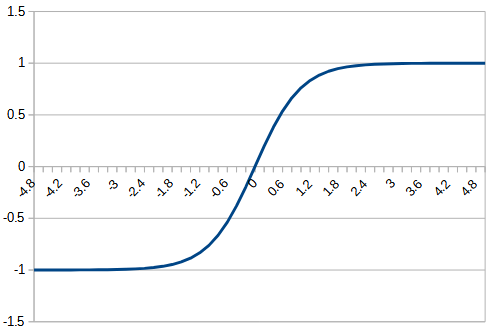 | 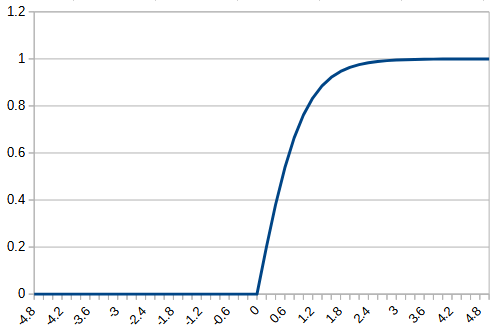 |
| accuracy | 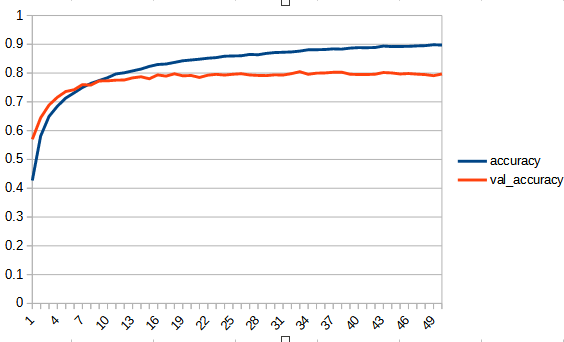 | 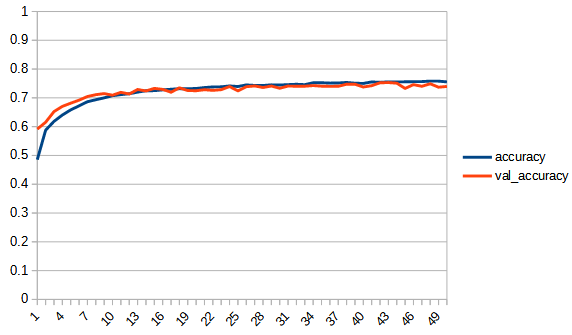 | 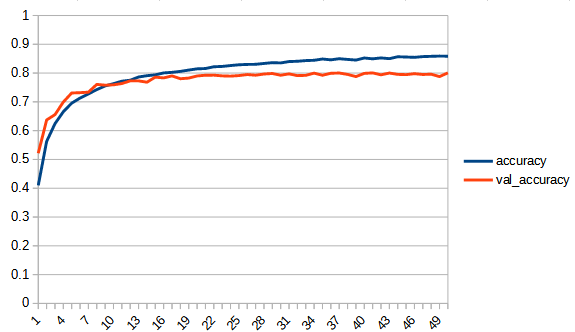 |
| loss | 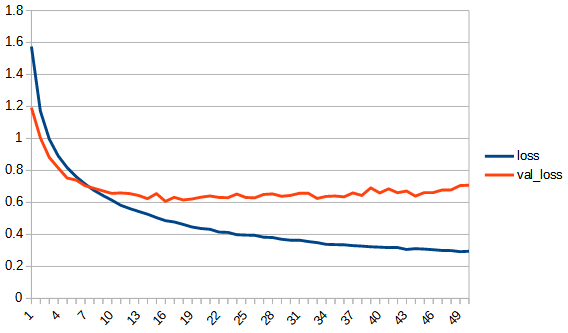 | 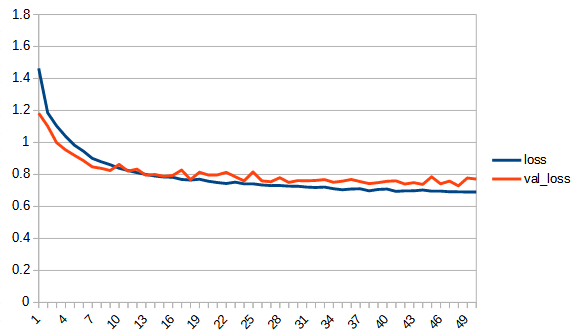 | 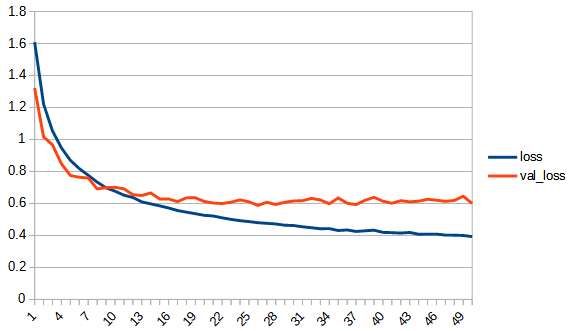 |
| csv | reluダウンロード | tanhダウンロード | rectified_tanhダウンロード |
| relu | sqrt_180_degree_symmetry g_a=0.1 | rectified_sqrt g_a = 0.1 | |
| function |  | 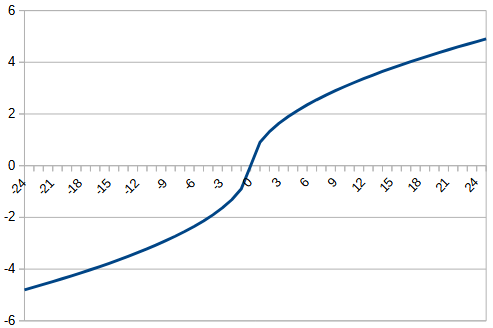 | 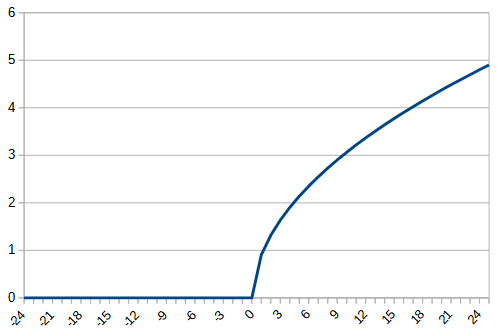 |
| accuracy |  | 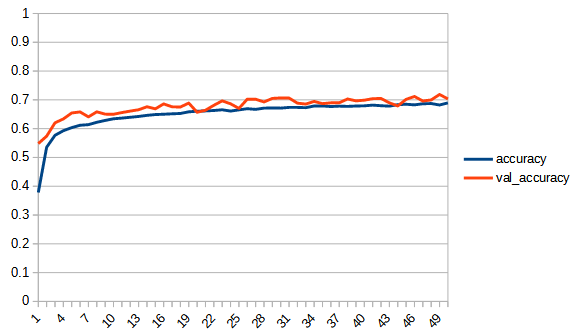 | 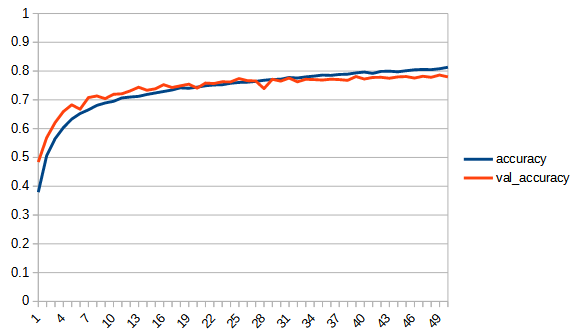 |
| loss |  | 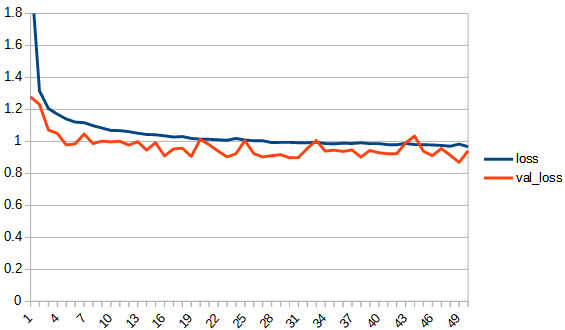 | 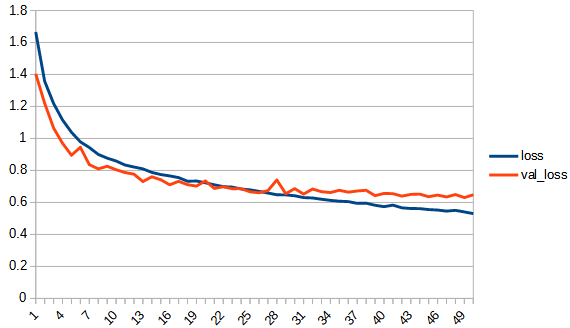 |
| csv | reluダウンロード | sqrt_01ダウンロード | rectified_sqrtダウンロード |
rectified_tanh:tanhと比べてaccuracy, loss 共にreluに近い形になっている。val_accuracyもtanhの7.5付近より大きくなり、reluとほぼ同じ0.8まで上がっている。tanhよりもval_…と無印の差が広がっており過学習の傾向が出ている。ただし、reluと比べると若干であるが過学習の傾向は少ないように見える。reluはval_lossが学習を重ねると増加傾向にあるが、rectified_tanhの方はその様子は見られない、
rectified_sqrt : reluとsqrt_180_degree_symmetryの中間的な性質といえる。sqrt_180_degree_symmetryよりも正答率が向上している。しかし、reluにはわずかに届いていない。学習の最後の方は若干過学習の傾向がみられるが、reluと比べるとその傾向は小さい。ただし、学習の進みが悪いだけのようにも見える。
結論:
tanh, sqrt 共に xが0以下の時 0 とする reluのような関数にした結果、どちらも正答率が向上した。このことから、0以下を常に0にすると正答率を上げることができるといえる。ただし、同時に過学習の傾向が現れる。
